当前位置:
首页 >
软件教程 >
六年级下册数学比例思维导图
六年级下册数学比例思维导图
迅捷思维导图
Web/PC/APP多端互通 支持多人协同编辑
迅捷思维导图
Web/PC/APP多端互通 支持多人协同编辑
《比例》是六年级下册数学所接触到的知识内容,是数学中的一个重要概念,主要涉及比例和比例关系计算的相关内容。通过学习比例单元,可以帮助我们更好地理解和应用数学知识,同时也为初中和高中数学的学习打下坚实的基础。
学习比例的过程中,可以用思维导图工具梳理比例的知识内容。通过绘制比例思维导图,可以借助思维导图有序发散的特点整理比例的相关知识内容。
一、为什么要画比例思维导图
比例思维导图可以帮助我们更好地理解和组织知识点的相关信息,其作用包括:
1、梳理思路:通过比例思维导图,可以将复杂的信息分解成更小的部分,帮助人们理解和组织信息,从而更好地梳理思路。
2、记忆信息:比例思维导图可以将信息以图像的形式呈现,这种视觉化的方式便于记忆和理解。通过不同颜色、图形和关键词的组合,帮助人们更好地记忆信息。
3、解决问题:比例思维导图可以帮助人们分析和解决问题。通过将问题分解成不同的部分,并将解决方案和结果与之相关联,便于找到问题的根源并提出解决方案。
4、表达思想:比例思维导图可以用于表达和分享思想。通过将各种信息和想法以图像的形式呈现,帮助他人理解和接受自己的思想或思路。
二、比例思维导图
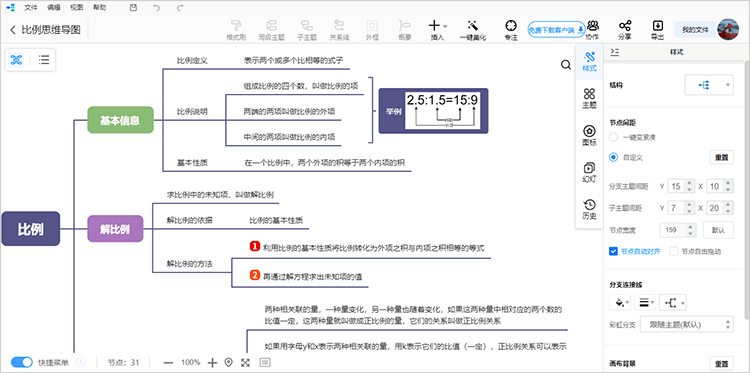
对于比例思维导图的绘制,首先可以对比例的相关知识内容进行梳理,接着将梳理好的比例知识内容有序呈现至思维导图工具内。
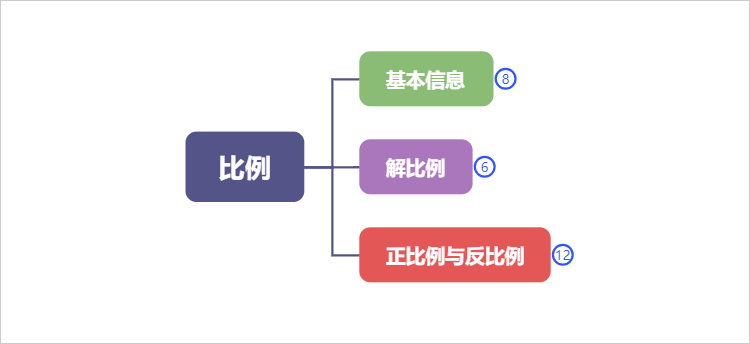
例如比例一节主要说明比例的基本信息、解比例、正比例与反比例三部分。我们将比例各部分内容以层层递进的方式有序呈现至思维导图内即可。
1、比例基本信息
2、解比例
3、正比例与反比例
1. 比例
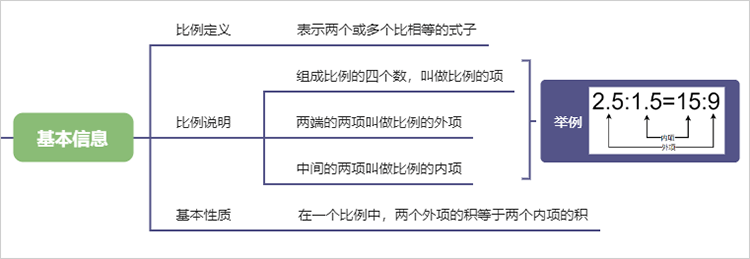
1.1. 基本信息
1.1.1. 比例定义
1.1.1.1. 表示两个或多个比相等的式子
1.1.2. 比例说明
1.1.2.1. 组成比例的四个数,叫做比例的项
1.1.2.2. 两端的两项叫做比例的外项
1.1.2.3. 中间的两项叫做比例的内项
1.1.3. 基本性质
1.1.3.1. 在一个比例中,两个外项的积等于两个内项的积
1.2. 解比例
1.2.1. 求比例中的未知项,叫做解比例
1.2.2. 解比例的依据
1.2.2.1. 比例的基本性质
1.2.3. 解比例的方法
1.2.3.1. 利用比例的基本性质将比例转化为外项之积与内项之积相等的等式
1.2.3.2. 再通过解方程求出未知项的值
1.3. 正比例与反比例
1.3.1. 正比例
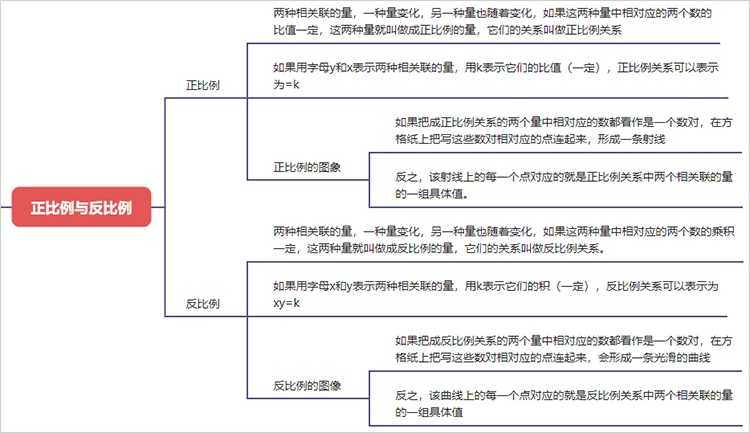
1.3.1.1. 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的比值一定,这两种量就叫做成正比例的量,它们的关系叫做正比例关系
1.3.1.2. 如果用字母y和x表示两种相关联的量,用k表示它们的比值(一定),正比例关系可以表示为=k
1.3.1.3. 正比例的图象
1.3.1.3.1. 如果把成正比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,形成一条射线
1.3.1.3.2. 反之,该射线上的每一个点对应的就是正比例关系中两个相关联的量的一组具体值。
1.3.2. 反比例
1.3.2.1. 两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
1.3.2.2. 如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以表示为xy=k
1.3.2.3. 反比例的图像
1.3.2.3.1. 如果把成反比例关系的两个量中相对应的数都看作是一个数对,在方格纸上把写这些数对相对应的点连起来,会形成一条光滑的曲线
1.3.2.3.2. 反之,该曲线上的每一个点对应的就是反比例关系中两个相关联的量的一组具体值
![迅捷活动banner]()